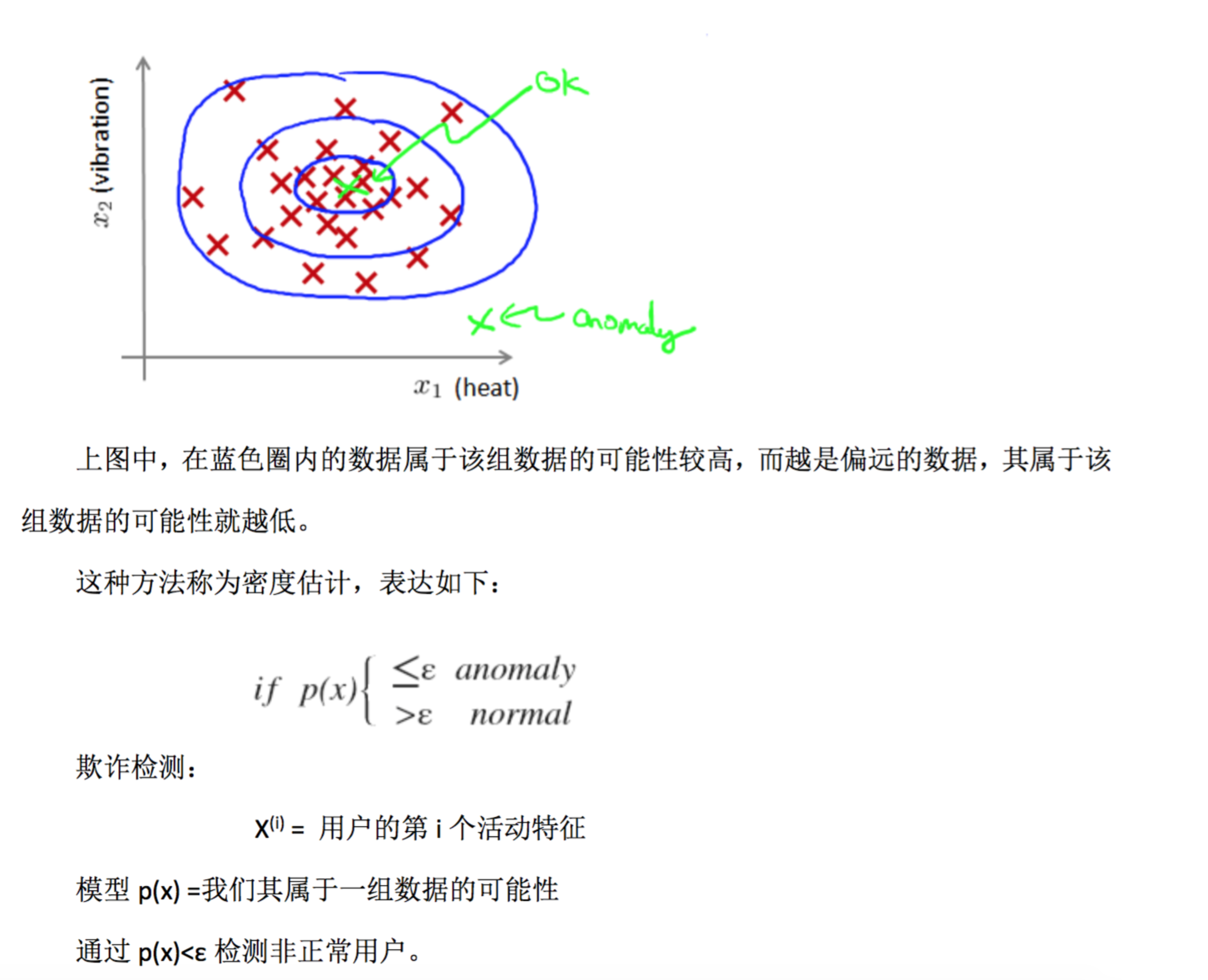
|
给定数据集 x(1),x(2),..,x(m),我们假使数据集是正常的,我们希望知道新的数据 xtest
是不 是异常的,即这个测试数据不属于该组数据的几率如何。我们所构建的模型应该能根据该测 试数据的位置告诉我们其属于一组数据的可能性 p(x)。
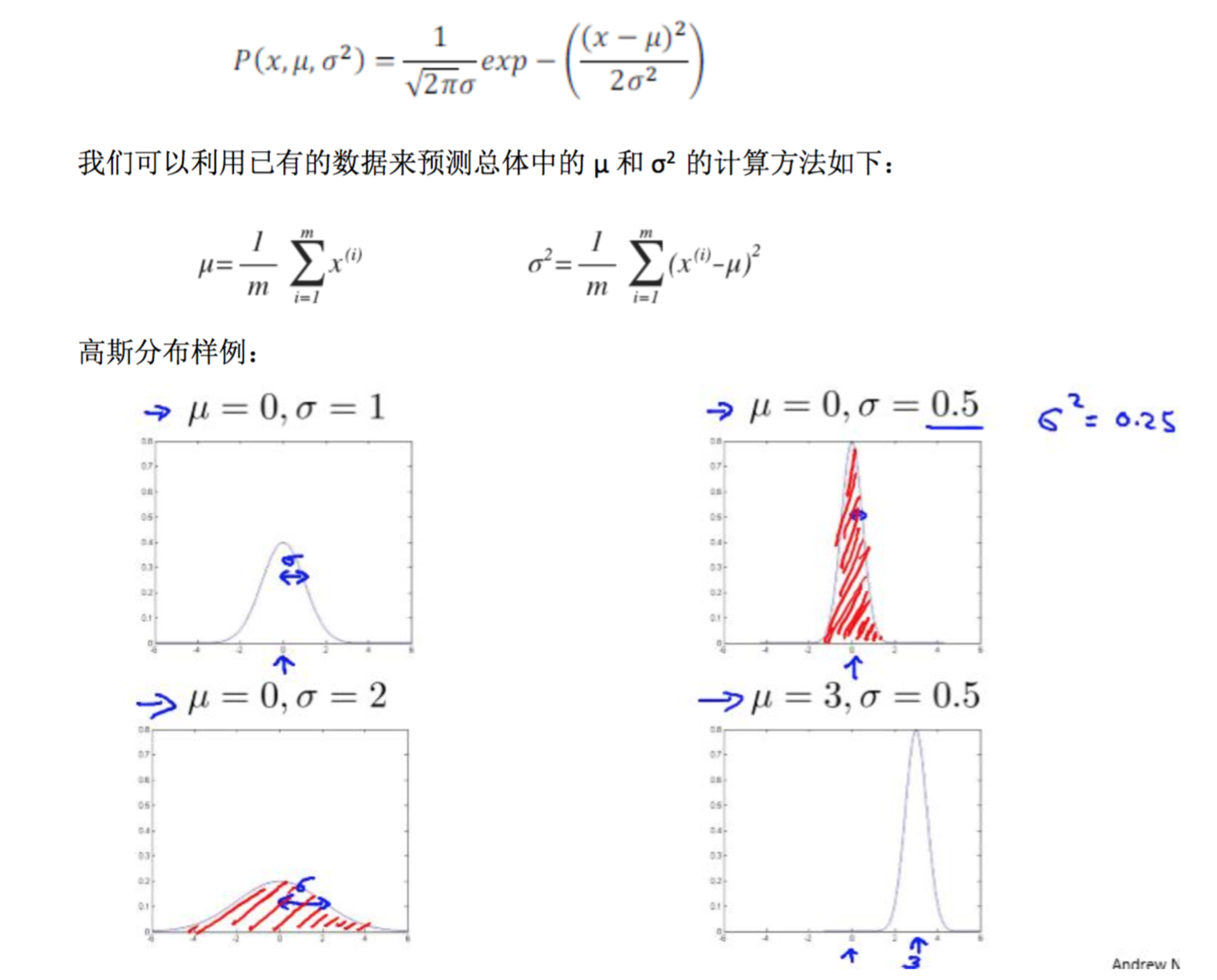
高斯分布 高斯分布,也称为正态分布。回顾高斯分布的基本知识。 通常如果我们认为变量 x 符合高斯分布 x~N(μ,σ2)则其概率密度函数为:
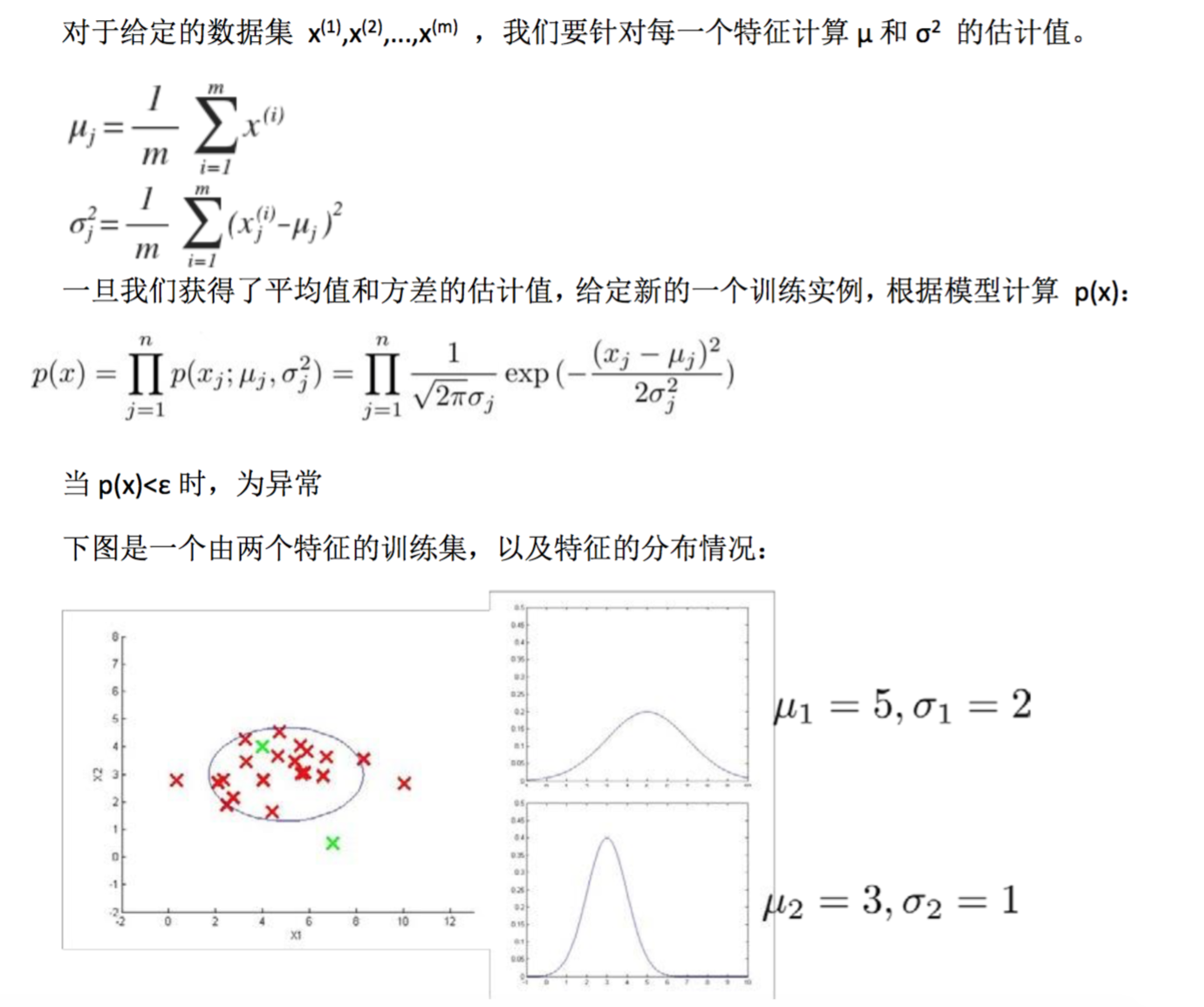
应用高斯分布开发异常检测算法
异常检测算法:
开发和评价一个异常检测系统
异常检测算法是一个非监督学习算法,意味着我们无法根据结果变量 y 的值来告诉我 们数据是否真的是异常的。我们需要另一种方法来帮助检验算法是否有效。当我们开发一个 异常检测系统时,我们从带标记(异常或正常)的数据着手,我们从其中选择一部分正常数 据用于构建训练集,然后用剩下的正常数据和异常数据混合的数据构成交叉检验集和测试 集。
例如:我们有 10000 台正常引擎的数据,有 20 台异常引擎的数据。 我们这样分配数 据:
6000 台正常引擎的数据作为训练集
2000 台正常引擎和 10 台异常引擎的数据作为交叉检验集 2000 台正常引擎和 10 台异常引擎的数据作为测试集 具体的评价方法如下:
- 根据测试集数据,我们估计特征的平均值和方差并构建 p(x)函数
- 对交叉检验集,我们尝试使用不同的 ε 值作为阀值,并预测数据是否异常,根据 F1 值或者查准率与查全率的比例来选择 ε
- 选出 ε 后,针对测试集进行预测,计算异常检验系统的 F1 值,或者查准率与查全 率之比
异常检测与监督学习对比
之前我们构建的异常检测系统也使用了带标记的数据,与监督学习有些相似,下面的对 比有助于选择采用监督学习还是异常检测: 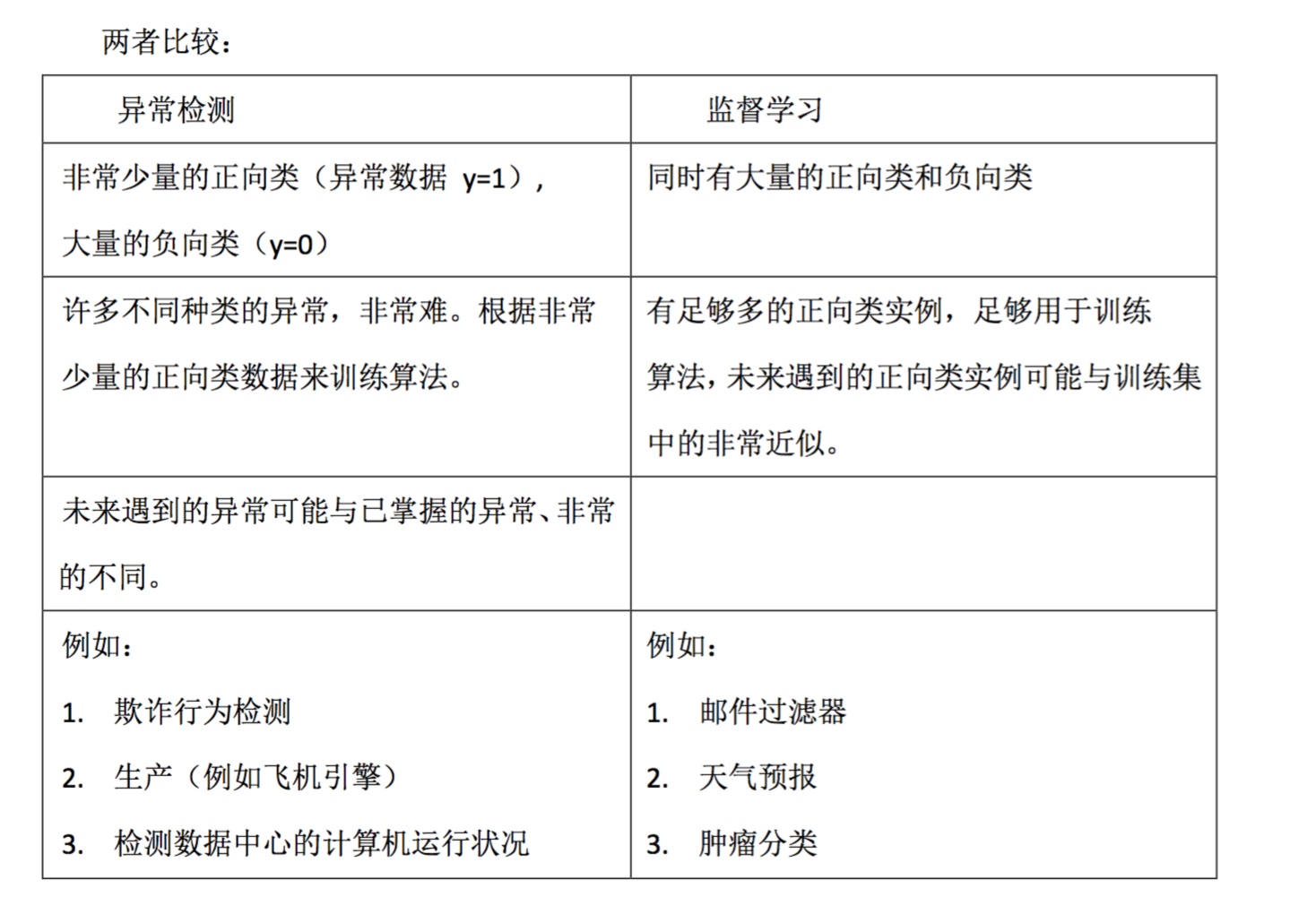
选择特征
对于异常检测算法,我们使用的特征是至关重要的,下面谈谈如何选择特征:
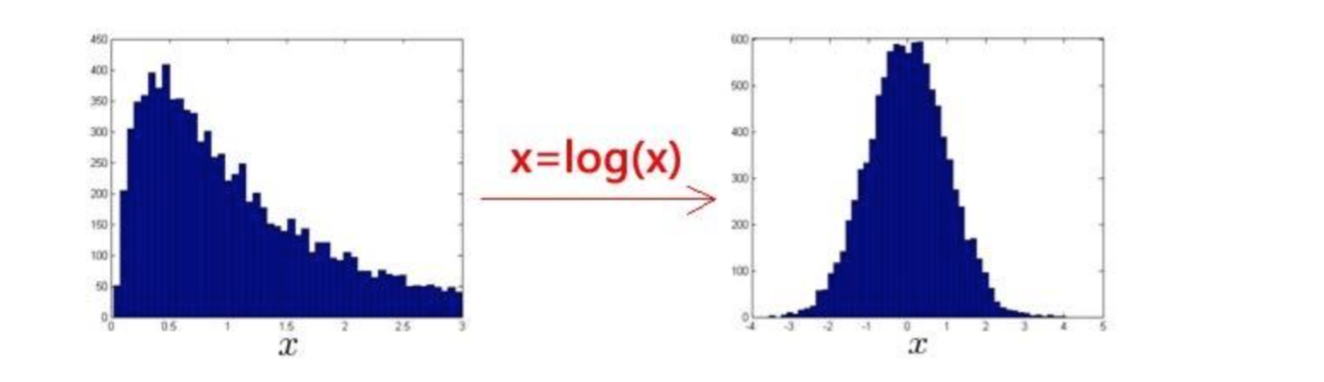
异常检测假设特征符合高斯分布,如果数据的分布不是高斯分布,异常检测算法也能够 工作,但是最好还是将数据转换成高斯分布,例如使用对数函数:x = log(x+c),其中 c 为非 负常数; 或者 x=xc
,c 为 0-1 之间的一个分数,等方法。
误差分析:
一个常见的问题是一些异常的数据可能也会有较高的 p(x)值,因而被算法认为是正常的。 这种情况下误差分析能够帮助我们,我们可以分析那些被算法错误预测为正常的数据,观察 能否找出一些问题。我们可能能从问题中发现我们需要增加一些新的特征,增加这些新特征 后获得的新算法能够帮助我们更好地进行异常检测。
我们通常可以通过将一些相关的特征进行组合,来获得一些新的更好的特征(异常数据 的该特征值异常地大或小),例如,在检测数据中心的计算机状况的例子中,我们可以用 CPU 负载与网络通信量的比例作为一个新的特征,如果该值异常地大,便有可能意味着该服务器 是陷入了一些问题中。
多元高斯分布
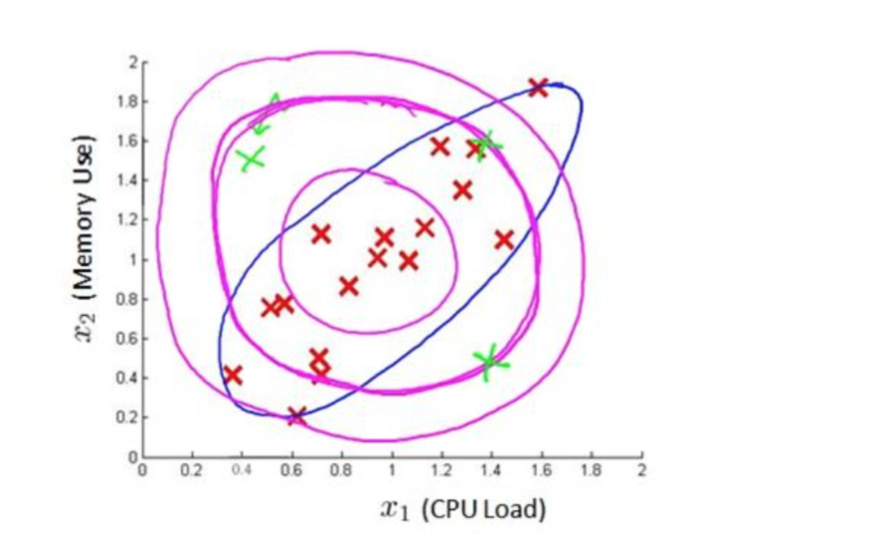
假使我们有两个相关的特征,而且这两个特征的值域范围比较宽,这种情况下,一般的 高斯分布模型可能不能很好地识别异常数据。其原因在于,一般的高斯分布模型尝试的是去 同时抓住两个特征的偏差,因此创造出一个比较大的判定边界。
下图中是两个相关特征,洋红色的线(根据 ε 的不同其范围可大可小)是一般的高斯分 布模型获得的判定边界,很明显绿色的 X 所代表的数据点很可能是异常值,但是其 p(x)值却 仍然在正常范围内。多元高斯分布将创建像图中蓝色曲线所示的判定边界。
在一般的高斯分布模型中,我们计算 p(x)的方法是: 通过分别计算每个特征对应的几 率然后将其累乘起来,在多元高斯分布模型中,我们将构建特征的协方差矩阵,用所有的特 征一起来计算 p(x)。
 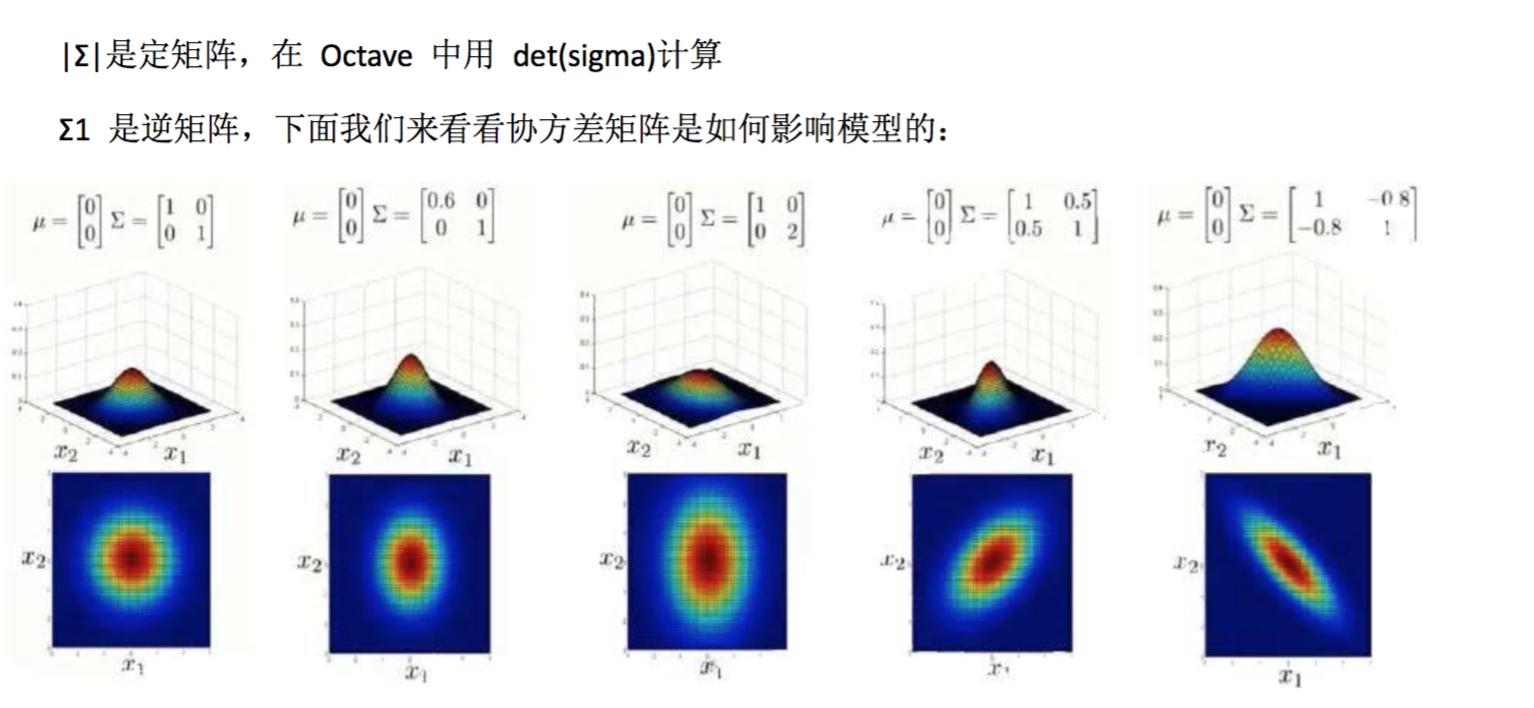
上图是 5 个不同的模型,从左往右依次分析:
- 是一个一般的高斯分布模型
- 通过协方差矩阵,令特征 1 拥有较小的偏差,同时保持特征 2 的偏差
- 通过协方差矩阵,令特征 2 拥有较大的偏差,同时保持特征 1 的偏差
- 通过协方差矩阵,在不改变两个特征的原有偏差的基础上,增加两者之间的正相关 性
- 通过协方差矩阵,在不改变两个特征的原有偏差的基础上,增加两者之间的负相关 性
多元高斯分布模型与原高斯分布模型的关系: 可以证明的是,原本的高斯分布模型是多元高斯分布模型的一个子集,即像上图中的第 1、2、3,3 个例子所示,如果协方差矩阵只在对角线的单位上有非零的值时,即为原本的 高斯分布模型了。
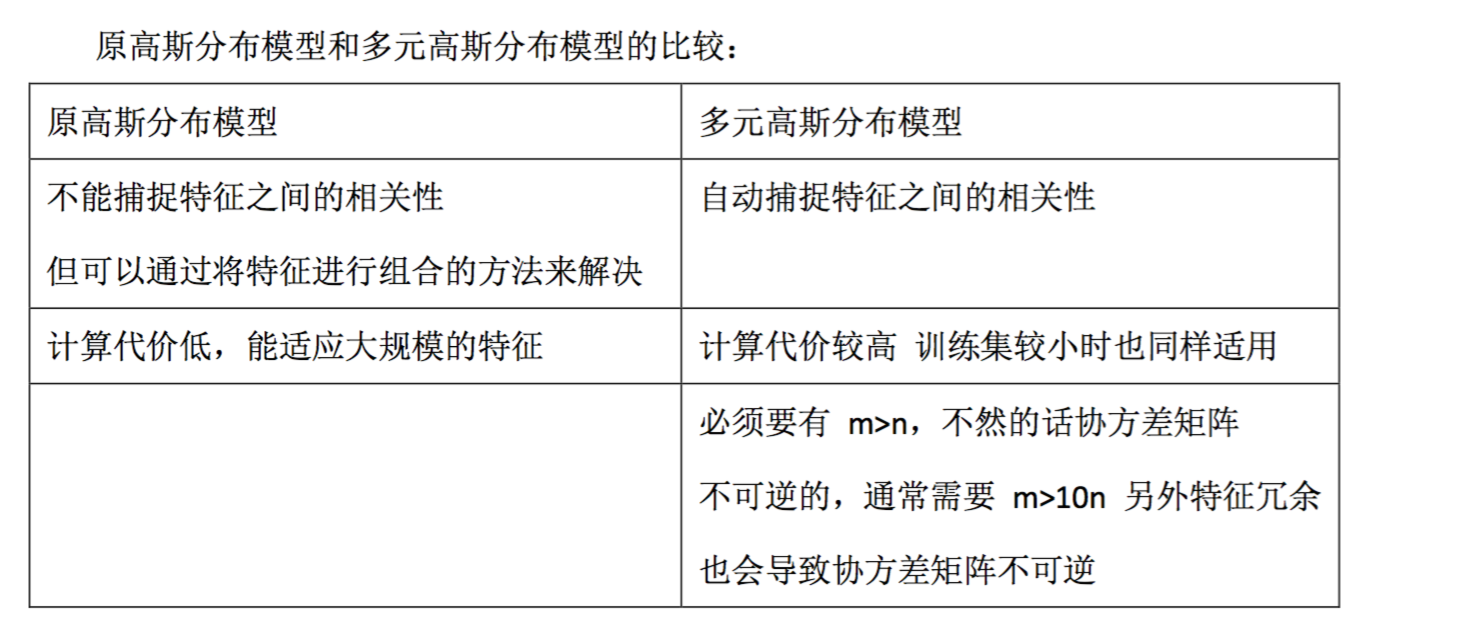
原高斯分布模型被广泛使用着,如果特征之间在某种程度上存在相互关联的情况,我们 可以通过构造新新特征的方法来捕捉这些相关性。 如果训练集不是太大,并且没有太多的特征,我们可以使用多元高斯分布模型。
摘自:http://whuhan2013.github.io/blog/2016/12/14/exception-and-recommd/
| 

 |手机版|小黑屋|Java自学者论坛
( 声明:本站文章及资料整理自互联网,用于Java自学者交流学习使用,对资料版权不负任何法律责任,若有侵权请及时联系客服屏蔽删除 )
|手机版|小黑屋|Java自学者论坛
( 声明:本站文章及资料整理自互联网,用于Java自学者交流学习使用,对资料版权不负任何法律责任,若有侵权请及时联系客服屏蔽删除 )