|
前言
以下内容是个人学习之后的感悟,转载请注明出处~
简介
在生活中,经常会遇到这样一个对象集,有个别的对象是与大部分对象不一样的,且前者是比较罕见的。我们通常
需要去发现它,这就用到了非监督学习的异常检测算法,下面来举一些异常检测的应用:
- 欺骗检测
- 制造业质检
- 动力环境监测
- .........
异常检测算法一般有以下几种:
许多异常检测技术首先建立一个数据模型,异常是那些同模型不能完美拟合的对象。例如,数据分布的模型可以
通过估计概率分布的参数来创建。如果一个对象不服从该分布,则认为他是一个异常。
通常可以在对象之间定义邻近性度量,异常对象是那些远离大部分其他对象的对象。当数据能够以二维或者三维散
布图呈现时,可以从视觉上检测出基于距离的离群点。
对象的密度估计可以相对直接计算,特别是当对象之间存在邻近性度量。低密度区域中的对象相对远离近邻,可能
被看做为异常。
异常检测算法分析
本文以基于模型的高斯分布异常检测算法为例,讲解异常检测的实现。
高斯分布,又名正态分布,其均值为μ、 方差为σ2的概率密度函数如下公式所示,如果一个随机变量X服从这个分布,我们写
作 X ~ N(μ,σ2)。此外,改变μ和σ,会使高斯分布曲线发生变化,其规律如下图所示:
-

-

首先,我们假设有一个数据集{x(1),x(2),x(3),.........,x(m)},其数据符合高斯分布,即 x(i)~ N(μ,σ2),那么我们可以得到如下公式:

根据数据集,可得出训练集:

利用上述训练集,求出每个特征对应的μj和σj,即可得到每个特征的概率密度函数p(xj;μj,σj),然后建立出异常检测模型:

最后取需要进行异常检测的数据,代入上述的模型公式,若p(x)<ε,则为异常值。
这里对异常检测算法的实现步骤做一下总结:

评估异常检测算法
我们采用的是查准率/召回率结合F-Score的评估方法,数据集分为训练集、验证集和测试集,这些都在之前学过的
机器学习之模型选择与改进中讲过,这里就不再赘述。
注意:ε值的选择一般来说得靠经验,或者可以选择不同的ε值,通过评估方法来选择最合适的值。
异常检测VS监督学习
异常检测的思想就是选出异类,其本质是分类,那么和监督学习相比,有什么区别呢?其区别如下图所示,总结的来说,
无非是当异常检测时,往往是异常点非常少的时候,根本无法用于监督学习,这也是使用异常检测的原因所在。

设计特征
上面提到的高斯分布异常检测算法,之所以能够达到我们想要的效果,是因为在数据集的特征都符合高斯分布的前提下,
一旦分布规律偏差很大,效果就会很差。所以我们需要对不满足高斯分布的特征进行重新设计,让其符合高斯分布,一般可以
通过对数转(log(x))进行转换。例如:
有时候我们还需要根据实际应用情况设计新的特征变量来帮助异常检测算法更好的检测离群点。举个检测网络系统的例子来
看看怎样设计出更合理的特征:
多元高斯分布
多元高斯分布有其优点也有其局限性,我们先来看看其优点。其优点是能够捕捉到上面模型捕捉不到的异常样本,
来看一个例子:
(1)我们的原始数据为下图所示(图左为二维的数据,图右为把两个特征分别当做高斯分布来建模)
(2)假如有个异常点(绿色样本点)如下图左中所示,其在下图右中的检测情况为:
从上图能够看出,这个绿色的异常样本在单独建模的模型中并不能检测出来。因此这就需要通过多元高斯分布构
建模型来检测。
多元高斯分布的概率密度函数为:
下面我们来看一些例子,来说明向量 和矩阵 和矩阵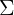 对概率密度函数的影响。
先来看 对概率密度函数的影响。
先来看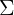 的影响: 的影响:
图一
图二
图三
从上面三个图中可以看出当矩阵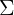 的副对角线都为0时,主对角线上的元素大小控制着概率密度函数俯瞰图的形状 的副对角线都为0时,主对角线上的元素大小控制着概率密度函数俯瞰图的形状
大小,至于具体到数字大小对应的形状,大家自己观察便知。
再来看看主对角线不变,变化副对角线是如何影响的例子:
图四
图五
能够看出,副对角线控制的是倾斜程度。
下面来看看 对概率密度函数的影响: 对概率密度函数的影响:
从上图能够看出 控制着图形的位置变化。 控制着图形的位置变化。
多元高斯分布在异常检测上的应用
介绍完多元高斯分布,下面我们来介绍下通过多元高斯分布推导出来的异常检测算法:
下面我们来看下多元高斯分布模型与多个一元高斯模型之间的关系:
其实就是当多元高斯分布模型的协方差矩阵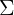 为对角矩阵,且对角线上的元素为各自一元高斯分布模型的方差时, 为对角矩阵,且对角线上的元素为各自一元高斯分布模型的方差时,
二者是等价的。
下面来总结比较下多元高斯分布模型和多个一元高斯分布模型:
以上是全部内容,如果有什么地方不对,请在下面留言,谢谢~ | 

 |手机版|小黑屋|Java自学者论坛
( 声明:本站文章及资料整理自互联网,用于Java自学者交流学习使用,对资料版权不负任何法律责任,若有侵权请及时联系客服屏蔽删除 )
|手机版|小黑屋|Java自学者论坛
( 声明:本站文章及资料整理自互联网,用于Java自学者交流学习使用,对资料版权不负任何法律责任,若有侵权请及时联系客服屏蔽删除 )